介绍

比较排序算法

冒泡排序（Bubble Sort）

介绍

冒泡排序 (bubble sort) 通过连续地比较与交换相邻元素实现排序。这个过程就像气泡从底部升到顶部一样， 因此得名冒泡排序。

冒泡过程可以利用元素交换操作来模拟：从数组最左端开始向右遍历，依次比较相邻元素大小，如果“左元素 > 右元素”就交换二者。遍历完成后，最大的元素会被移动到数组的最右端。

算法流程

设数组的长度为 𝑛 ，冒泡排序的步骤: 挨个计较相邻的数字将最大的数字排在最后

  • 首先，对 𝑛 个元素执行“冒泡”，将数组的最大元素交换至正确位置
  • 接下来，对剩余 𝑛 − 1 个元素执行“冒泡”，将第二大元素交换至正确位置
  • 以此类推，经过 𝑛 − 1 轮“冒泡”后，前 𝑛 − 1 大的元素都被交换至正确位置
  • 仅剩的一个元素必定是最小元素，无须排序，因此数组排序完成

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 冒泡排序
bool swapped;
do {
    swapped = true;
    for (size_t i = 1; i < v.size(); i++) {
        if (v[i - 1] > v[i]) {
            swap(v[i - 1], v[i]);
            swapped = false;
        }
    }
} while (!swapped);

//bubble sort
bool swapped;
for (int i = 9;i > 0;i --){
    swapped = false;
    for (int j = 0;j < i;j ++){
        if (arr[j] > arr[j+1]){
            swap(arr[j],arr[j+1]);
            swapped = true;
        }
    }
    if(!swapped) break;
}

算法特性

  • 时间复杂度为 O(n2)、自适应排序：各轮“冒泡”遍历的数组长度依次为 n−1、n−2、…、2、1 ，总和为 (n−1)n/2 。在引入 flag 优化后，最佳时间复杂度可达到 O(n) 。
  • 空间复杂度为 O(1)、原地排序：指针 i 和 j 使用常数大小的额外空间。
  • 稳定排序：由于在“冒泡”中遇到相等元素不交换

选择排序（Selection Sort）

介绍

选择排序（Selection Sort) 开启一个循环，每轮从未排序区间选择最小的元素，将其放到已排序区间的末尾。

算法流程

  • 初始状态下，所有元素未排序，即未排序（索引）区间为 [0,n−1]
  • 选取区间 [0,n−1] 中的最小元素，将其与索引 0 处的元素交换。完成后，数组前 1 个元素已排序。
  • 选取区间 [1,n−1] 中的最小元素，将其与索引 1 处的元素交换。完成后，数组前 2 个元素已排序。
  • 以此类推。经过 n−1 轮选择与交换后，数组前 n−1 个元素已排序。
  • 仅剩的一个元素必定是最大元素，无须排序，因此数组排序完成。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* 选择排序 */
void selectionSort(vector<int> &nums) {
    int n = nums.size();
    // 外循环：未排序区间为 [i, n-1]
    for (int i = 0; i < n - 1; i++) {
        // 内循环：找到未排序区间内的最小元素
        int k = i;
        for (int j = i + 1; j < n; j++) {
            if (nums[j] < nums[k])
                k = j; // 记录最小元素的索引
        }
        // 将该最小元素与未排序区间的首个元素交换
        swap(nums[i], nums[k]);
    }
}

算法特性

  • 时间复杂度为 O(n2)、非自适应排序：外循环共 n−1 轮，第一轮的未排序区间长度为 n ，最后一轮的未排序区间长度为 2 ，即各轮外循环分别包含 n、n−1、…、3、2 轮内循环，求和为 (n−1)(n+2)2 。
  • 空间复杂度为 O(1)、原地排序：指针 i 和 j 使用常数大小的额外空间。
  • 非稳定排序：如图 11-3 所示，元素 nums[i] 有可能被交换至与其相等的元素的右边，导致两者的相对顺序发生改变。

插入排序（Insertion Sort）

介绍

算法流程

代码实现

算法特性

快速排序（Quick Sort）

归并排序（Merge Sort）

希尔排序（Shell Sort）

堆排序（Heap Sort）

非比较排序算法

桶排序（bucket sort）

介绍

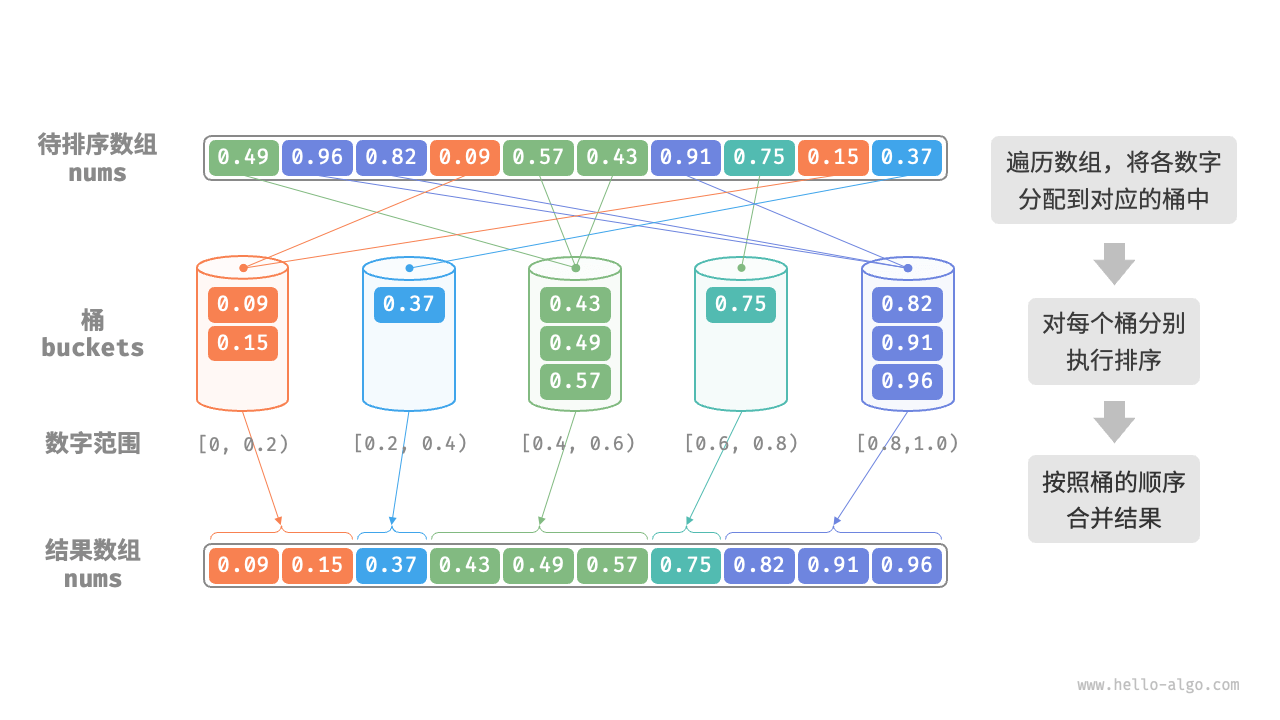
桶排序（bucket sort）是分治策略的一个典型应用。它通过设置一些具有大小顺序的桶，每个桶对应一个数据范围，将数据平均分配到各个桶中；然后，在每个桶内部分别执行排序；最终按照桶的顺序将所有数据合并。

算法流程

考虑一个长度为 n 的数组，其元素是范围 [0,1) 内的浮点数

  • 初始化 k 个桶，将 n 个元素分配到 k 个桶中。

  • 对每个桶分别执行排序（这里采用编程语言的内置排序函数）

  • 按照桶从小到大的顺序合并结果。

代码实现

1

计数排序（Counting Sort）

基数排序